domingo, 17 de noviembre de 2019
miércoles, 13 de noviembre de 2019
Agujeros de gusano
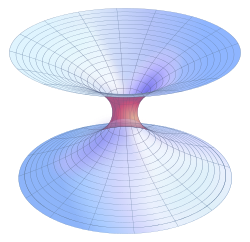
Agujero de gusano
Esquema de un agujero de gusano que técnicamente permite el viaje a través del tiempo. Si uno de los dos extremos del puente atravesado por la línea verde está en movimiento, seguir la ruta roja y volver al punto inicial según en sentido opuesto a la ruta verde podría permitir volver atrás en el tiempo, ya que el espacio-tiempo representado contendría curvas temporales cerradas.
Cuando una estrella supergigante roja explota, arroja materia al exterior, de modo que acaba siendo de un tamaño inferior y se convierte en una estrella de neutrones. Pero también puede suceder que se comprima tanto que absorba su propia energía en su interior y desaparezca dejando un agujero negro en el lugar que ocupaba. Este agujero tendría una gravedad tan grande que ni siquiera la radiación electromagnética podría escapar de su interior. Estaría rodeado por una frontera esférica, llamada horizonte de sucesos. La luz traspasaría esta frontera para entrar, pero no podría salir, por lo que el agujero visto desde grandes distancias debería ser completamente negro (aunque Stephen Hawking postuló que ciertos efectos cuánticos generarían la llamada radiación de Hawking). Dentro del agujero, los astrofísicos conjeturan que se forma una especie de cono sin fondo. En 1994, el telescopio espacial Hubble detectó la presencia de uno muy denso en el centro de la galaxia elíptica M87, pues la alta aceleración de gases en esa región indica que debe de haber un objeto 3 500 millones de veces más masivo que el Sol. Finalmente, este agujero terminará por absorber a la galaxia entera.[1]
El primer científico en advertir de la existencia de agujeros de gusano fue el austríaco Ludwig Flamm, en 1916. En este sentido, la hipótesis del agujero de gusano es una actualización de la decimonónica teoría de una cuarta dimensión espacial que suponía —por ejemplo—, dado un cuerpo toroidal en el que se podían encontrar las tres dimensiones espaciales comúnmente perceptibles, una cuarta dimensión espacial que abreviara las distancias y, de esa manera, los tiempos de viaje. Esta noción inicial fue planteada de manera más científica en 1921 por el matemático alemán Hermann Weyl, sin embargo, no usó el término "agujero de gusano" (habló de "tubos unidimensionales"), cuando este relacionó sus análisis de la masa en términos de la energía de un campo electromagnético[2] con la teoría de la relatividad de Albert Einstein publicada en 1916.
En la actualidad, la teoría de cuerdas admite la existencia de más de tres dimensiones espaciales (ver hiperespacio), pero esas dimensiones extra estarían compactadas a escalas subatómicas (según la teoría de Kaluza-Klein), por lo que parece muy difícil (si no imposible) aprovecharlas para emprender viajes en el espacio y el tiempo.
Índice
Origen del nombre
El término «agujero de gusano» fue introducido por el físico teórico estadounidense John Wheeler en 1957 (inspirado en la obra de Weyl) en un artículo de 1957 co-escrito con Charles Misner:Proviene de la siguiente analogía usada para explicar el fenómeno: si el universo es la piel de una manzana y un gusano viaja sobre su superficie, la distancia de un punto de la manzana a su antípoda es igual a la mitad de la circunferencia de la manzana, siempre que el gusano permanezca sobre la superficie de esta. Pero si, en vez de esto, el gusano cavara un agujero directamente a través de la manzana, la distancia que tendría que recorrer sería considerablemente menor, ya que la distancia más cercana entre dos puntos es una línea recta que une a ambos.
Tipos de agujero de gusano
- Los agujeros de gusano del intrauniverso conectan una posición de un universo con otra posición del mismo universo en un tiempo diferente. Un agujero de gusano debería poder conectar posiciones distantes en el universo por plegamientos espaciotemporales, de manera que permitiría viajar entre ellas en un tiempo menor que el que tomaría hacer el viaje a través del espacio normal.
- Los agujeros de gusano del interuniverso asocian un universo con otro diferente y se denominan «agujeros de gusano de Schwarzschild». Esto permite especular sobre si tales agujeros de gusano podrían usarse para viajar de un universo a otro paralelo. Otra aplicación de un agujero de gusano podría ser el viaje en el tiempo. En ese caso, sería un atajo para desplazarse de un punto espaciotemporal a otro. En la teoría de cuerdas, un agujero de gusano es visto como la conexión entre dos D-branas, donde las bocas están asociadas a las branas y conectadas por un tubo de flujo. Se cree que los agujeros de gusano son una parte de la espuma cuántica o espaciotemporal.
- Los agujeros de gusano euclídeos, estudiados en física de partículas.
- Los agujeros de gusano de Lorentz, principalmente estudiados en relatividad general y en gravedad semiclásica. Dentro de estos destacan los agujeros de gusano atravesables, un tipo especial de agujero de gusano de Lorentz que permitiría a un ser humano viajar de un lado al otro del agujero.
- El agujero de gusano de Schwarzschild supuestamente formado por un agujero negro de Schwarzschild, que se considera infranqueable.
- El agujero de gusano supuestamente formado por un agujero negro de Reissner-Nordstrøm o Kerr-Newman, que resultaría franqueable, pero en una sola dirección, y que podría contener un agujero de gusano de Schwarzschild.
- El agujero de gusano de Lorentz, que posee masa negativa y se estima franqueable en ambas direcciones (pasado y futuro).
Agujeros de gusano de Schwarzschil
Los agujeros de gusano de Lorentz, conocidos como agujeros de gusano de Schwarzschild o puentes de Einstein-Rosen, son nexos que unen áreas de espacio que puede ser modeladas como soluciones de vacío en las ecuaciones de campo de Einstein por unión de un modelo de agujero negro y uno de agujero blanco. Esta solución fue hallada por Albert Einstein y su compañero Nathan Rosen, que publicó primero el resultado en 1935. Sin embargo, en 1962, John A. Wheeler y Robert W. Fuller publicaron un artículo en el que divulgaban la demostración de que este tipo de agujero de gusano es inestable y se desintegraría instantáneamente tan pronto como se formase.
Antes de que los problemas de estabilidad de los agujeros de gusano de Schwarzschild se hiciesen evidentes, se propuso que los cuásares podían ser agujeros blancos, de modo que formaban las zonas terminales de los agujeros de gusano de este tipo. Sin embargo, investigaciones recientes descartan que los cuásares sean equiparables a los agujeros blancos.
Los agujeros de gusano de Schwarzschild inspiraron a Kip Thorne a imaginar el tránsito por ellos mediante la sujeción de su garganta y su apertura por medio de materia exótica (de masa y energía negativas).
Agujeros de gusano practicables
Los agujeros de gusano practicables de Lorentz, también llamados atravesables, permitirían viajar no solo de una parte del universo a otra, sino incluso de un universo a otro. Los agujeros de gusano conectan dos puntos del espacio-tiempo, por lo que permitirían el viaje tanto en el espacio como en el tiempo. En la teoría de la relatividad general, la posibilidad de atravesar agujeros de gusano fue demostrada por primera vez por Kip S. Thorne y su graduado Mike Morris en un artículo publicado en 1988. El tipo de agujero de gusano atravesable que ellos descubrieron se mantendría abierto por una especie de concha esférica de materia exótica denominada agujero de gusano de Morris-Thorne. Posteriormente se han descubierto otros tipos de agujeros de gusano atravesables, como uno que se mantiene abierto por cuerdas cósmicas, ya hipotetizado antes por Matt Visser en un artículo publicado en 1989.
Fuente: Wikipedia
Los agujeros blancos
Agujero blanco
Agujero blanco es el término propuesto para definir una solución de las ecuaciones del campo gravitatorio de Einstein, cuya existencia se cree imposible, debido a las condiciones tan especiales que requiere.
Se trata de una región finita del espacio-tiempo, visible como objeto celeste con una densidad tal que deforma el espacio pero que, a diferencia del agujero negro, deja escapar materia y energía en lugar de absorberla. De hecho ningún objeto puede permanecer en el interior de dicha región durante un tiempo infinito. Por ello se define un agujero blanco como el reverso temporal de un agujero negro: el agujero negro absorbe a su interior a la materia en cambio el agujero blanco la expulsa.
Los más importantes avances en esta teoría son debidos a los trabajos independientes de los matemáticos Ígor Nóvikov y Yuval Ne'eman en la década de 1960, basados en la solución de Kruskal-Schwarzschild de las ecuaciones de la relatividad general.
El agujero negro de Schwarzschild es descrito como una singularidad en la cual una geodésica puede solo ingresar, tal tipo de agujero negro incluye dos tipos de horizonte: un horizonte "futuro" (es decir, una región de la cual no se puede salir una vez que se ha ingresado en ella, y en la cual el tiempo -con el espacio- son curvados hacia el futuro), y un horizonte "pasado", el horizonte pasado tiene por definición la de una región donde es imposible la estancia y de la cual sólo se puede salir; el horizonte pasado entonces ya correspondería a un agujero blanco1
En el caso de un agujero negro de Reißner-Nordstrøm el agujero blanco pasa a ser —por ahora siempre hipotéticamente— la "salida" de un agujero negro en otro "universo", es decir, otra región asintóticamente plana similar a la región de la que procede un objeto emergente por ese otro tipo de agujero. La carga eléctrica del agujero del Reissner-Nordstrøm proporciona un mecanismo físico más razonable para construir posibles agujeros blancos.
Hipótesis varias
A diferencia de los agujeros negros para los cuales existe un proceso físico bien estudiado, el colapso gravitatorio (que da lugar a agujeros negros cuando una estrella algo más masiva que el sol agota su "combustible" nuclear), no hay un proceso análogo claro que lleve con seguridad a producir agujeros blancos. Aunque se han apuntado algunas hipótesis:
- Los agujeros blancos como una especie de "salida" de los agujeros negros, ambos tipos de singularidades probablemente estarían conectadas por un agujero de gusano (notar que, como los agujeros blancos, los agujeros de gusano aún no han sido encontrados hasta ahora); cuando se descubrieron los cuásares se supuso que estos eran los buscados agujeros blancos pero en la actualidad tal supuesto ha sido descartado.2
- Otra idea generalizada en la actualidad es que los agujeros blancos serían muy inestables, durarían muy poco tiempo e incluso tras formarse podrían colapsar y transformarse en agujeros negros.
- También se ha llegado a conjeturar que la singularidad inicial del big bang pudo haber sido una especie de agujero blanco en sus momentos iniciales.
Fuente: Wikipedia
viernes, 27 de septiembre de 2019
Proyecto del teodolito
Hola, hoy les voy a compartir el cómo, cuándo y por qué de la realización del proyecto de creación de un teodolito casero, de parte de yo y unos compañeros del 5°"B" de secundaria del Liceo Naval Germán Astete. :v
Objetivo:
Se busca, mediante este trabajo, facilitar la medición de ángulos verticales de elevación o depresión de modo que se puedan aplicar las propiedades pitagóricas y trigonométricas para el calculo de medidas de difícil medición manual.
Razones trigonométricas:
Ángulos verticales:
Materiales:
1 tubo de plástico o cartón
1 plomada
Pegamento
Papel
Lápiz
Procedimiento de creación:
1º Paso: Pintar los materiales de negro, amarrar los tres palos y procurar que quede fuerte para que no se pueda soltar, después de esto abrirlos.2º Paso: Colocar el vaso en la parte superior de los tres palos con la puntilla introducida por el medio de éste, pero antes colocar en el vaso un palo de balso para su aseguramiento.
3º Paso: Colocar la base y buscar la estabilidad del teodolito.
5º Paso: Cortar el palo de balso en 4 partes iguales, formando una "Y" ponemos el rollo del papel ayudado de los chinches entre dos palos luego procedemos a introducir la puntilla en el transportador completo para así poder realizar el movimiento de arriba y hacia abajo.
6º Paso : Cogemos el nivel y le echamos un poquito de silicona lo colocamos al teodolito para que nos de un buen nivel y nos de las medidas exactas.
7º Paso :Cogemos el transportador medio calculamos de donde sale el punto medio del teodolito que es 180º y entonces le agregamos un poquito de silicona y lo ponemos en uno delos extremos y así podemos mostrar los grados hacia los lados.
El trabajo:
Tuvimos la tarea de calcular con ayuda del teodolito la altura de la parte superior del segundo piso del colegio y la de un poste. Primero, colocamos el teodolito frente a las estructuras y medimos la distancia de separación de sus bases con la del trabajo con la ayuda de una wincha.
Luego, calculamos el ángulo de elevación que poseía nuestra herramienta con respecto de ambas cimas. Entonces, tras obtener el ángulo, multiplicamos su tangente por la distancia de separación, de modo que encontramos el valor de sus alturas. Todo ello, con las correcciones e indicaciones de nuestro profesor del área.
1. El transportador no estuvo recto en más de una ocasión por lo que teníamos resultados erróneos
Galería de fotos:(Salimos bellos)
jueves, 11 de julio de 2019
Suscribirse a:
Entradas (Atom)